Egyptian Circle Area Formula

https://www.geogebra.org/classic/udxzy

Do you know how the Egyptians approximate the area of a circle?

They might be drawing a lot of squares and try to determine the best fit, a square that is close to the area of a circle.

And then upon determining the best square, they compare the side (s) of such square to the diameter of the circle and derived this beautiful mathematical derivation for the area of the circle:

Egyptian's Area of the Circle Formula

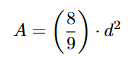
Now, bring oneself back to the time of the Egyptians the modern way using GeoGebra and by moving the slider side (s) of the square, determine the best square that would fit the area of a circle by setting the error percentage to 1%.

Please determine the side length (s) of the square that would approximate the area of the circle according to the Egyptians.

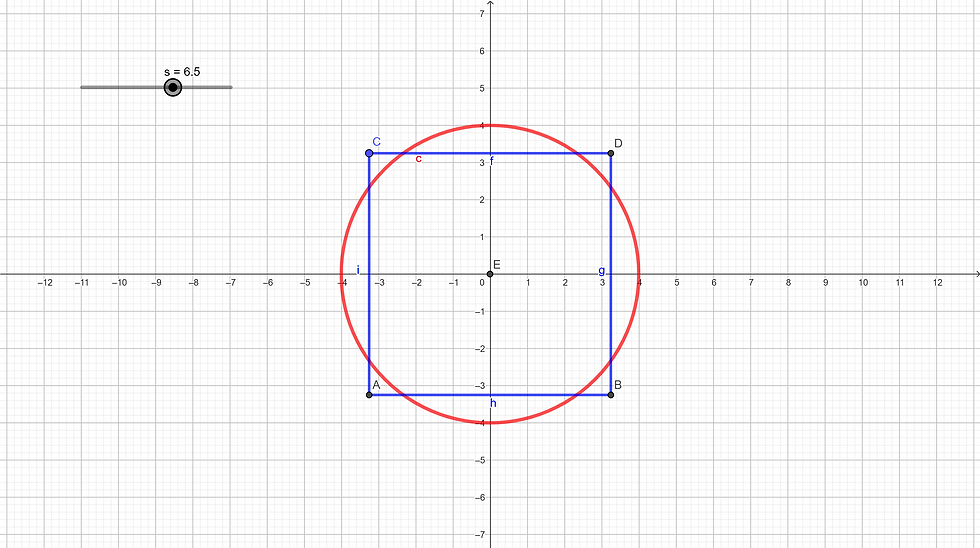
What is the length of the side (s) of such square?

Explore in the algebra pane the code for such computation.

Have fun!

Thank you for your kind support.