Eigen Values and Eigen Vectors

https://www.geogebra.org/classic/dcy4h78s

Use GeoGebra to determine the square matrix, calculate its Eigenvalues, and find the corresponding Eigenvectors. Pair each Eigenvalue with its corresponding Eigenvector.

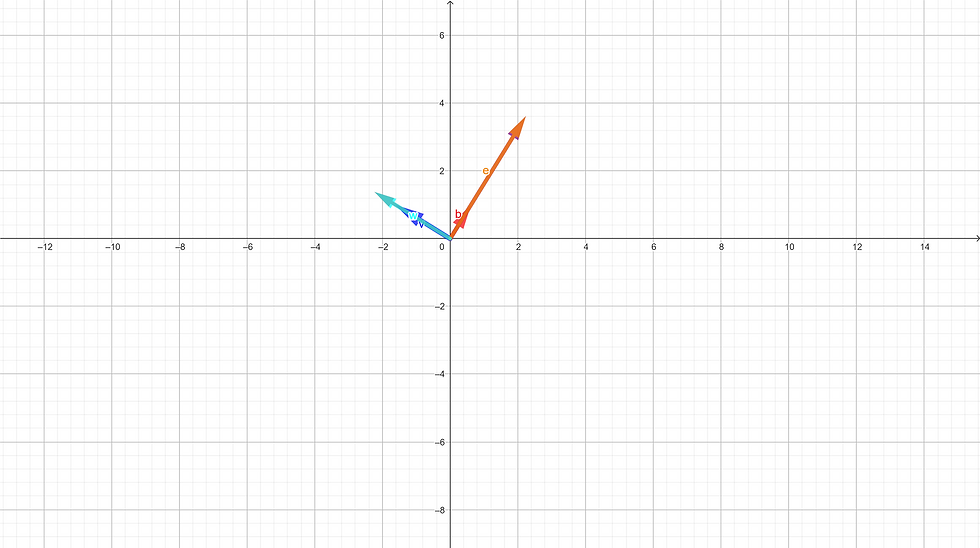
Findings/Conclusion:

A square matrix A acts on an Eigenvector by scaling it according to its corresponding Eigenvalue. The Eigenvalue is the scalar that determines how much the Eigenvector is stretched or shrunk when multiplied by the matrix. Thus, the square matrix A scales the Eigenvector by the Eigenvalue.